MATH5714 Linear Regression, Robustness and Smoothing
University of Leeds, Semester 1, 2024/25
Preface
The MATH5714M module includes all the material from MATH3714 (Linear Regression and Robustness), plus additional material on “Smoothing”.
From MATH3714 (and from previous modules) we know how to fit a regression line through points \((x_1, y_1), \ldots, (x_n, y_n) \in\mathbb{R}^2\). The underlying model there is described by the equation \[\begin{equation*} y_i = \alpha + \beta x_i + \varepsilon_i \end{equation*}\] for all \(i \in \{1, 2, \ldots, n\}\), and the aim is to find values for the intercept \(\alpha\) and the slope \(\beta\) such that the residuals \(\varepsilon_i\) are as small as possible. This procedure, linear regression, and its extensions are discussed in the level 3 component of the module.
In the level 5 component of this module, we will discuss “smoothing” which is a
technique which can be used when linear models are no longer appropriate for
the data. An example of such a situation is illustrated in figure
0.1. The red line in this figure is obtained using one of the
smoothing techniques which we will discuss in the level 5 part of the module.
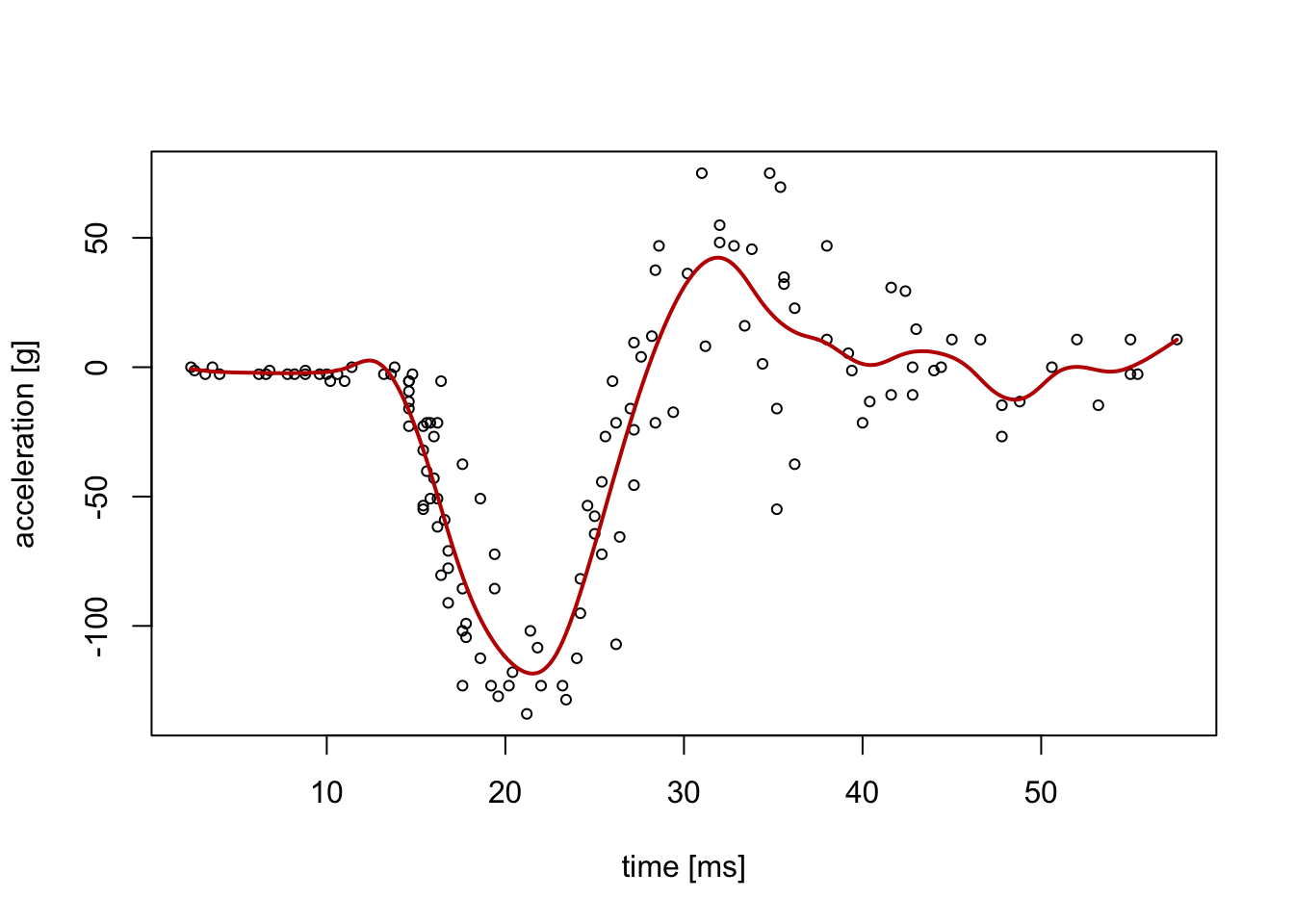
Figure 0.1: An illustration of a dataset where a linear (straight line) model is not appropriate. The data represents a series of measurements of head acceleration in a simulated motorcycle accident, used to test crash helmets (the mcycle dataset from the MASS R package).