Section 1 Kernel Density Estimation

In this section, we suppose we are given data \(x_1,\ldots, x_n \in\mathbb{R}\) from an unknown probability density \(f\), and our goal is to estimate \(f\) from the data.

1.1 Probability Densities

Before we consider how to estimate a density, let us recall what a density is. A random variable \(X \in \mathbb{R}\) has density \(f\colon \mathbb{R}\to [0, \infty)\) if \[\begin{equation*} P\bigl(X \in [a,b]\bigr) = \int_a^b f(x) \,dx \end{equation*}\] for all \(a, b\in\mathbb{R}\) with \(a < b\). Densities are also called “probability densities” or “probability density functions”.

Graphically, the integral \(\int_a^b f(x) \,dx\) can be interpreted as the area under the graph of \(f\). This is illustrated in figure 1.1.

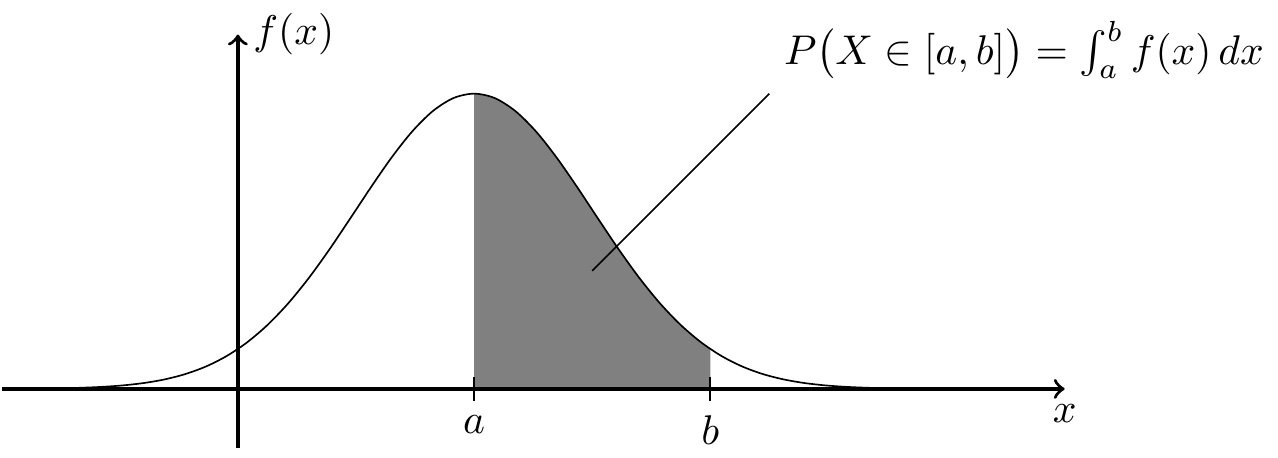
An illustration of how the area under the graph of a density can be interpreted as a probability.

Figure 1.1: An illustration of how the area under the graph of a density can be interpreted as a probability.

A function \(f\) is the density of a random variable \(X\) if and only if \(f \geq 0\) and \[\begin{equation*} \int_{-\infty}^\infty f(x) \,dx = 1. \end{equation*}\] In the following, we will see how to estimate \(f\) from data.

1.2 Histograms

A commonly used technique to approximate the density of a sample is to plot a histogram. To illustrate this, we use the faithful dataset built into R, which contains waiting times between eruptions and the duration of the eruption for the Old Faithful geyser in the Yellowstone National Park. (You can type help(faithful) in R to learn more about this dataset.) Here we focus on the waiting times only. A simple histogram for this dataset is shown in figure 1.2.

x <- faithful$waiting
hist(x, probability = TRUE,
     main = NULL, xlab = "time between eruptions [mins]")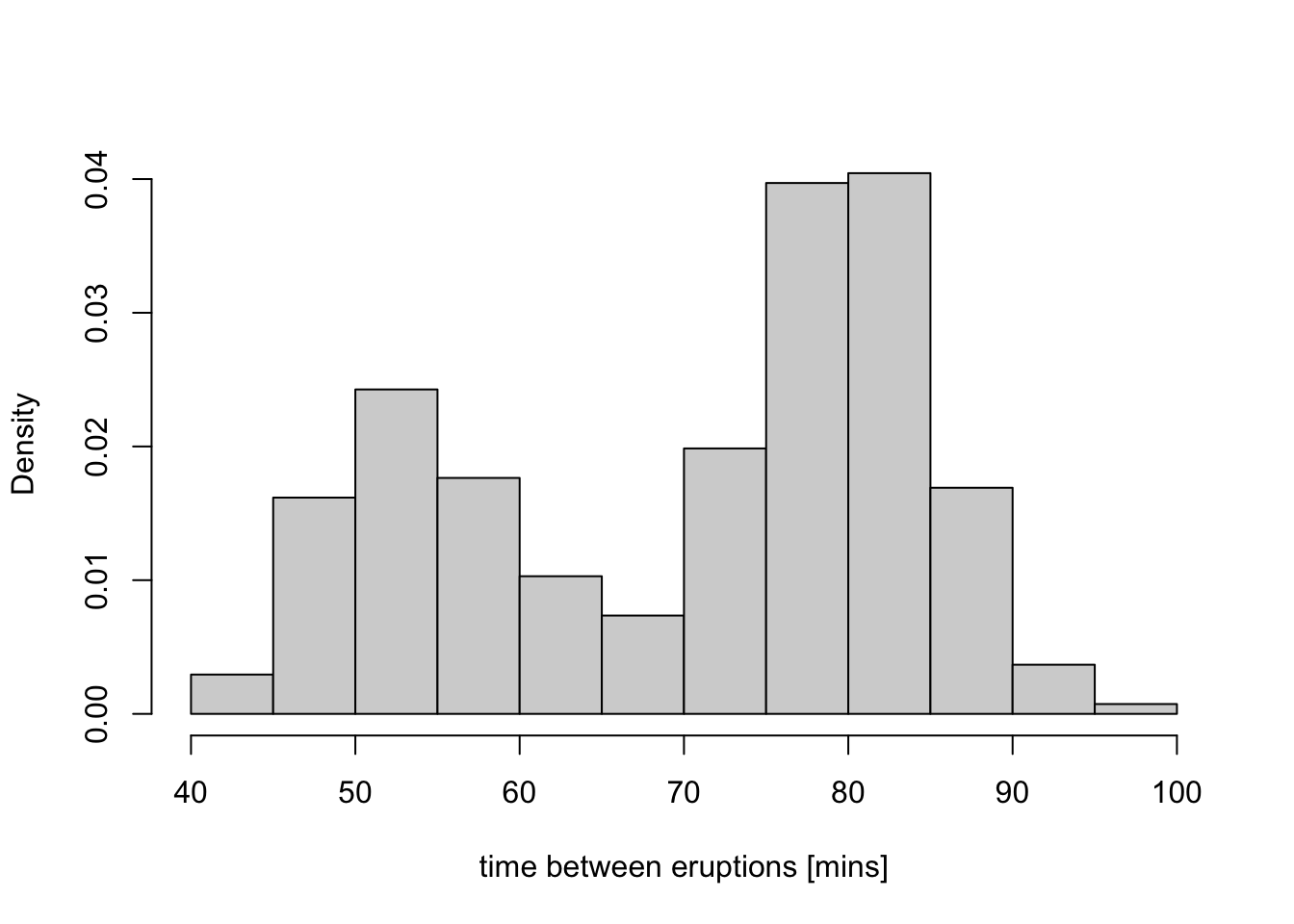
This figure shows how a histogram can be used to approximate a probability density. From the plot one can see that the density of the waiting times distribution seems to be bi-modal with peaks around 53 and 80 minutes.

Figure 1.2: This figure shows how a histogram can be used to approximate a probability density. From the plot one can see that the density of the waiting times distribution seems to be bi-modal with peaks around 53 and 80 minutes.

The histogram splits the data range into “buckets”, with bar heights proportional to the number of samples in each bucket.

As we have seen, the area under the graph of the density \(f\) over the interval \([a, b]\) corresponds to the probability \(P\bigl(X \in [a,b]\bigr)\). For the histogram to approximate the density, we need to scale the height \(h_{a,b}\) of the bucket \([a, b]\) so that the area in the histogram is also close to this probability. Since we don’t know the probability \(P\bigl(X \in [a,b]\bigr)\) exactly, we have to approximate it as \[\begin{equation*} P\bigl(X \in [a,b]\bigr) \approx \frac{n_{a,b}}{n}, \end{equation*}\] where \(n_{a,b}\) is the number of samples in the bucket \([a,b]\), and \(n\) is the total number of samples. So we need \[\begin{align*} (b-a) \cdot h_{a,b} &= \mbox{area of the histogram bar} \\ &\approx \mbox{area of the density} \\ &= P\bigl(X \in [a,b]\bigr) \\ &\approx \frac{n_{a,b}}{n}. \end{align*}\] and thus we choose \[\begin{equation*} h_{a,b} = \frac{1}{(b - a) n} n_{a,b}. \end{equation*}\]

We can write the count \(n_{a,b}\) as a sum over the data: \[\begin{equation*} n_{a,b} = \sum_{i=1}^n I_{[a,b]}(x_i), \end{equation*}\] where \(I_{[a,b]}(x) = 1\) if \(x \in [a,b]\) and \(I_{[a,b]}(x) = 0\) otherwise. Substituting this into the formula for the histogram, we get \[\begin{equation} h_{a,b} = \frac{1}{n} \sum_{i=1}^n \frac{1}{b - a} I_{[a,b]}(x_i). \tag{1.1} \end{equation}\] This shows that the histogram can be written as an average of indicator functions.

Histograms have several limitations:

  • Histograms are only meaningful if the buckets are chosen well. If the buckets are too large, not much of the structure of \(f\) can be resolved. If the buckets are too small, the estimate \(P\bigl(X \in [a,b]\bigr) \approx n_{a,b}/n\) will be poor and the histogram will no longer resemble the shape of \(f\).
  • Even if reasonable bucket sizes are chosen, the result can depend quite strongly on the exact locations of these buckets.
  • Histograms have sharp edges at bucket boundaries, creating discontinuities in the density estimate even when the true density \(f\) is smooth.

Kernel density estimation addresses these issues by using smooth weight functions, called “kernels”, that gradually decrease as we move away from \(x\). Each sample \(x_i\) contributes to the estimate at \(x\) with a weight that depends on the distance \(|x - x_i|\). Nearby samples get higher weight, distant samples get lower weight, and the transition is smooth.

1.3 Kernels

To make this idea precise, we first define what we mean by a kernel.

Definition 1.1 A kernel is a function \(K\colon \mathbb{R}\to \mathbb{R}\) such that

  • \(\int_{-\infty}^\infty K(x) \,dx = 1\),
  • \(K(x) = K(-x)\) (i.e. \(K\) is symmetric) and
  • \(K(x) \geq 0\) (i.e. \(K\) is positive) for all \(x\in \mathbb{R}\).

The first condition ensures that \(K\) must decay as \(|x|\) becomes large. The second condition, symmetry, ensures that \(K\) is centred around \(0\), and the third condition, positivity, makes \(K\) a probability density. (While most authors list all three properties shown above, sometimes the third condition is omitted.)

There are many different kernels in use. Some examples are listed below; a more exhaustive list is available on Wikipedia.

  • Uniform Kernel: \[\begin{equation*} K(x) = \begin{cases} 1/2 & \mbox{if $-1 \leq x \leq 1$} \\ 0 & \mbox{otherwise} \end{cases} \end{equation*}\]

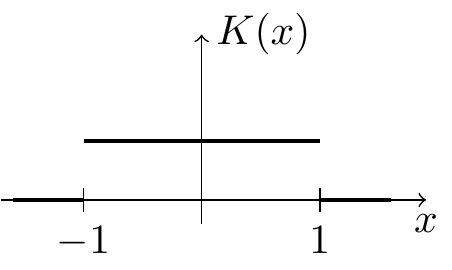
  • Triangular Kernel: \[\begin{equation} K(x) = \begin{cases} 1-|x| & \mbox{if $-1 \leq x \leq 1$} \\ 0 & \mbox{otherwise} \end{cases} \tag{1.2} \end{equation}\]

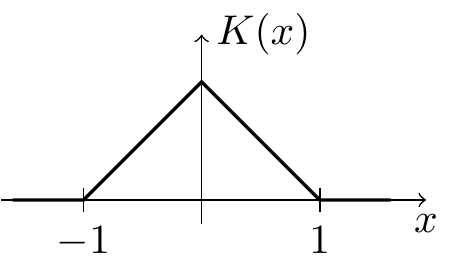
  • Epanechnikov Kernel: \[\begin{equation*} K(x) = \begin{cases} \frac34 (1-x^2) & \mbox{if $-1 \leq x \leq 1$} \\ 0 & \mbox{otherwise} \end{cases} \end{equation*}\]

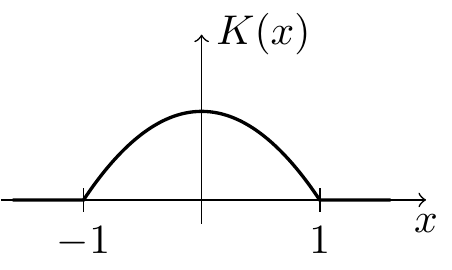
  • Gaussian Kernel: \[\begin{equation*} K(x) = \frac{1}{\sqrt{2\pi}} \exp\bigl(-x^2/2\bigr) \end{equation*}\]

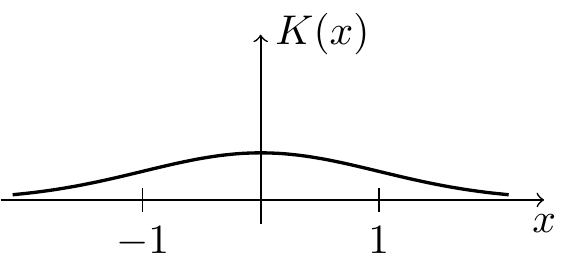
The “width” of the kernel determines how smooth the resulting estimate is. A narrow kernel gives more weight to nearby samples and produces a more detailed (but potentially noisier) estimate, while a wider kernel averages over more distant samples and produces a smoother estimate.

To control the width, we use a bandwidth parameter \(h > 0\) and define the rescaled kernel \(K_h\) by \[\begin{equation*} K_h(y) = \frac{1}{h} K(y/h) \end{equation*}\] for all \(y\in \mathbb{R}\). The bandwidth parameter \(h\) controls the width: small \(h\) gives a narrow kernel, large \(h\) gives a wide kernel.

Lemma 1.1 If \(K\) is a kernel, then \(K_h\) is also a kernel.

Proof. We need to verify the three properties from definition 1.1. Using the substitution \(z = y/h\) we find \[\begin{align*} \int_{-\infty}^\infty K_h(y) \,dy &= \int_{-\infty}^\infty \frac{1}{h} K(y/h) \,dy \\ &= \int_{-\infty}^\infty \frac{1}{h} K(z) \,h \,dz \\ &= \int_{-\infty}^\infty K(z) \,dz \\ &= 1. \end{align*}\] For the second property, we have \[\begin{equation*} K_h(-y) = \frac{1}{h} K(-y/h) = \frac{1}{h} K(y/h) = K_h(y), \end{equation*}\] where we used the symmetry of \(K\). Finally, since \(K(y/h) \geq 0\) for all \(y\), we also have \(K_h(y) = \frac{1}{h} K(y/h) \geq 0\) for all \(y\).

Remark. Note that the choice of kernel \(K\) and bandwidth \(h\) is not unique. For a given kernel shape, different authors use different normalisations. For example, we could replace our triangular kernel \(K\) from equation (1.2) with \(\tilde K(x) = K(x/\sqrt{6}) / \sqrt{6}\), which has variance 1. If we simultaneously replace \(h\) with \(\tilde h = h/\sqrt{6}\), then the rescaled kernel remains unchanged: \(\tilde K_{\tilde h} = K_h\).

1.4 Kernel Density Estimation

We can now define the kernel density estimate.

Definition 1.2 For a kernel \(K\), bandwidth \(h > 0\) and \(x \in \mathbb{R}\), the kernel density estimate for \(f(x)\) is given by \[\begin{equation*} \hat f_h(x) = \frac{1}{n} \sum_{i=1}^n K_h(x - x_i), \end{equation*}\] where \(K_h\) is the rescaled kernel defined above.

Note the similarity to the histogram formula (1.1): both are averages of weight functions applied to the data. The key difference is that the kernel \(K_h(x - x_i)\) is centred around each data point \(x_i\), whereas the indicator function \(I_{[a,b]}(x_i)\) is fixed at the bucket location \([a,b]\).

Similar to the bucket width in histograms, the bandwidth parameter \(h\) controls how smooth the density estimate \(\hat f_h\) is: small \(h\) gives narrow kernels that put weight only on very nearby samples, while large \(h\) gives wide kernels that average over more distant samples.

Later sections will discuss how to choose the kernel \(K\) for good properties. Note that if \(K\) is continuous, then \(K_h\) and \(\hat f_h\) are also continuous.

1.5 Kernel Density Estimation in R

Kernel density estimates can be computed in R using the built-in density() function. If x is a vector containing the data, then density(x) computes a basic kernel density estimate, using the Gaussian kernel. The function has a number of optional arguments, which can be used to control details of the estimate:

  • bw = ... can be used to control the bandwidth \(h\). If no numeric value is given, a heuristic is used. Note that for some kernels, bw differs from our \(h\) by a constant factor. The value bw=1 always corresponds to the case where the probability distribution with density \(K_h\) has variance 1.

  • kernel = ... can be used to choose the kernel. Choices include "rectangular" (the uniform kernel), "triangular", "epanechnikov" and "gaussian". The default value is "gaussian".

See help(density) for details.

To illustrate the use of density(), we use a dataset about the annual amount of snow falling in Buffalo, New York for different years:

# downloaded from https://teaching.seehuhn.de/data/buffalo/
x <- read.csv("data/buffalo.csv")
snowfall <- x$snowfall

The return value of density is an R object which contains information about the kernel density estimate.

m <- density(snowfall)
str(m)
## List of 8
##  $ x         : num [1:512] -4.17 -3.72 -3.26 -2.81 -2.35 ...
##  $ y         : num [1:512] 4.28e-06 4.94e-06 5.68e-06 6.50e-06 7.42e-06 ...
##  $ bw        : num 9.72
##  $ n         : int 109
##  $ old.coords: logi FALSE
##  $ call      : language density.default(x = snowfall)
##  $ data.name : chr "snowfall"
##  $ has.na    : logi FALSE
##  - attr(*, "class")= chr "density"

The fields $x and $y contain the \(x\) and \(y\) coordinates, respectively, of points on the \(x \mapsto \hat f_h(x)\) curve, which approximates \(f\). The field $bw shows the numeric value for the bandwidth chosen by the heuristic. The returned object can also directly be used as an argument to plot() and lines(), to add the graph of \(\hat f_h\) to a plot.

The following code illustrates the use of density() with different bandwidth parameters. The result is shown in figure 1.3.

par(mfrow = c(2,2))

for (bw in c(1, 2, 4, 8)) {
  plot(density(snowfall, bw = bw, kernel = "triangular", n = 1000),
    xlim = c(25,200),
    ylim = c(0, 0.025),
    xlab = paste("bandwidth =", bw),
    main = NA)
}
This figure illustrates how the bandwidth of a kernel density estimate can be controlled in R.

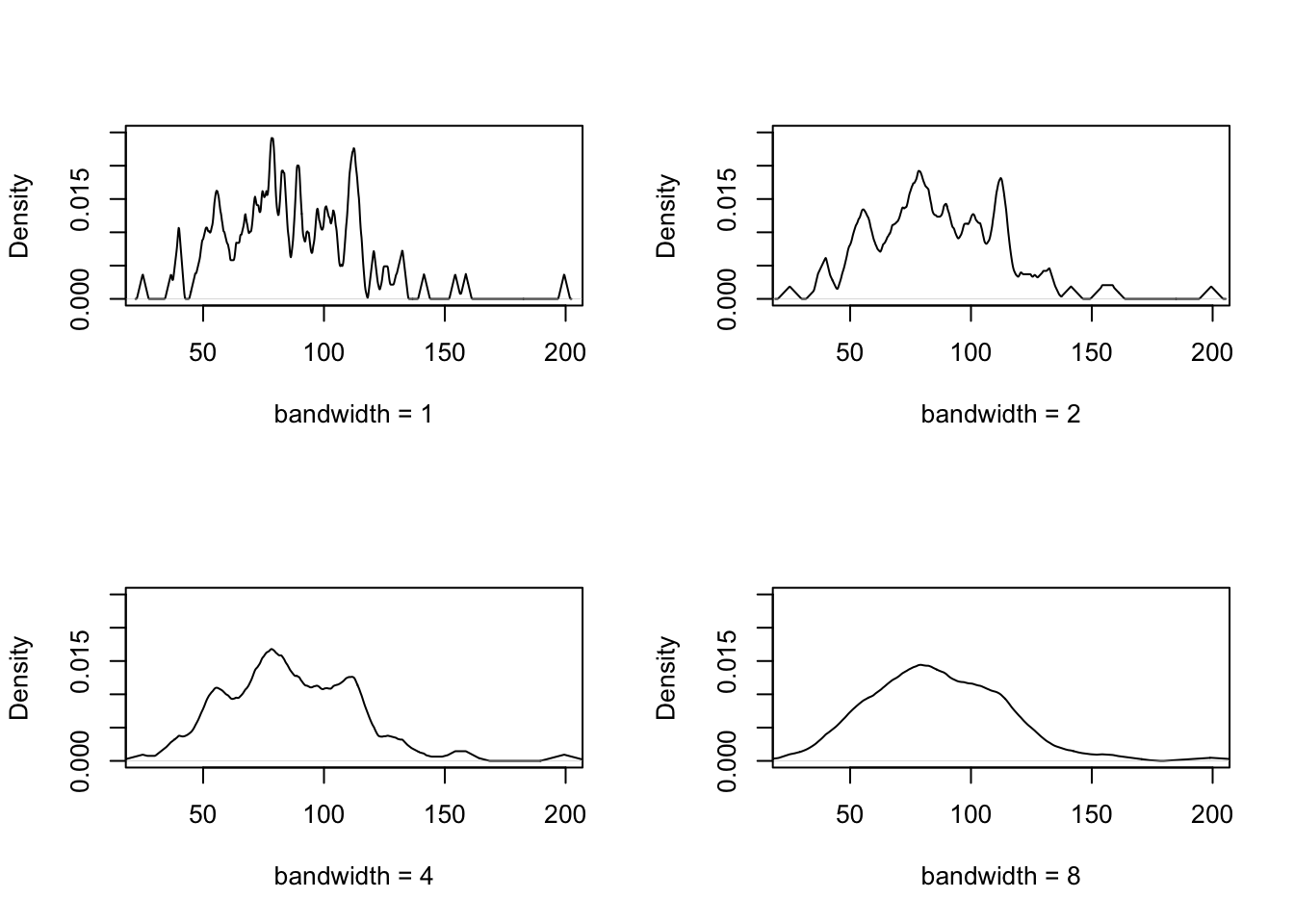
Figure 1.3: This figure illustrates how the bandwidth of a kernel density estimate can be controlled in R.

Summary

  • Histograms approximate densities using indicator functions on fixed buckets.
  • Kernel density estimates replace fixed buckets with smooth kernels centred on each data point.
  • The bandwidth parameter controls the smoothness of the kernel density estimate.
  • In R, the density() function computes kernel density estimates.