Section 3 Kernel Density Estimation in Practice

In this section we conclude our discussion of kernel density estimation by considering different aspects which are important when using the method in practice.

3.1 Optimal Bandwidth

The two terms on the right-hand side of (2.11) are balanced in that the first term decreases for large \(h\) while the second term decreases for small \(h\). By taking derivatives with respect to \(h\), we can find the optimal value of \(h\). Ignoring the higher order terms, we get \[\begin{equation*} \frac{\partial}{\partial h} \mathop{\mathrm{MSE}}\nolimits\bigl( \hat f_h(x) \bigr) = -\frac{1}{nh^2} f(x) R(K) + \mu_2(K)^2 f''(x)^2 h^3 \end{equation*}\] and thus the derivative equals zero, if \[\begin{equation*} \frac{1}{nh^2} f(x) R(K) = \mu_2(K)^2 f''(x)^2 h^3 \end{equation*}\] or, equivalently, \[\begin{equation*} h = h_\mathrm{opt} := \Bigl( \frac{f(x) R(K)}{n \mu_2(K)^2 f''(x)^2} \Bigr)^{1/5}. \end{equation*}\] It is easy to check that this \(h\) corresponds to the minimum of the MSE. This shows how the optimal bandwidth depends both on the kernel and on the target density \(f\). In practice, this formula is hard to use, since \(f''\) is unknown. (We don’t even know \(f\)!)

Substituting the optimal value of \(h\) back into equation (2.11), we get \[\begin{align*} \mathop{\mathrm{MSE}}\nolimits_\mathrm{opt} &= \frac{1}{n} f(x) R(K) \Bigl( \frac{n \mu_2(K)^2 f''(x)^2}{f(x) R(K)} \Bigr)^{1/5} + \frac14 \mu_2(K)^2 f''(x)^2 \Bigl( \frac{f(x) R(K)}{n \mu_2(K)^2 f''(x)^2} \Bigr)^{4/5} \\ &= \frac54 \; \frac{1}{n^{4/5}} \; \Bigl( R(K)^2 \mu_2(K) \Bigr)^{2/5} \; \Bigl( f(x)^2 |f''(x)| \Bigr)^{2/5}. \end{align*}\] This expression clearly shows the contribution of \(n\), \(K\) and \(f\):

  • If the bandwidth is chosen optimally, as \(n\) increases the bandwidth \(h\) decreases proportionally to \(1/n^{1/5}\) and the MSE decreases proportionally to \(1 / n^{4/5}\). For comparison, in a Monte Carlo estimate for an expectation, the MSE decreases proportionally to \(1/n\). The error in kernel density estimation decreases slightly slower than for Monte Carlo estimates.

  • The error is proportional to \(\bigl( R(K)^2 \mu_2(K) \bigr)^{2/5}\). Thus we should use kernels where the value \(R(K)^2 \mu_2(K)\) is small.

  • The error is proportional to \(f(x)^2 |f''(x)|\). We cannot influence this term, but we can see that \(x\) where \(f\) is large or has high curvature have higher estimation error.

3.2 Choice of Kernel

The integrated error in equation (2.12) is proportional to \(\bigl( R(K)^2 \mu_2(K) \bigr)^{2/5}\), and none of the remaining terms in the equation depends on the choice of the kernel. Thus, we can minimise the error by choosing a kernel which has minimal \(R(K)^2 \mu_2(K)\). For a given kernel, it is easy to work out the value of \(R(K)^2 \mu_2(K)\).

Example 3.1 For the uniform kernel we have \[\begin{equation*} K(x) = \begin{cases} 1/2 & \mbox{if $-1 \leq x \leq 1$} \\ 0 & \mbox{otherwise.} \end{cases} \end{equation*}\] From this we find \[\begin{equation*} R(K) = \int_{-\infty}^\infty K(x)^2 \,dx = \int_{-1}^1 \frac14 \,dx = \frac12 \end{equation*}\] and \[\begin{equation*} \mu_2(K) = \int_{-\infty}^\infty x^2 K(x) \,dx = \int_{-1}^1 \frac12 x^2 \,dx = \frac16 \Bigl. x^3 \Bigr|_{x=-1}^1 = \frac16 \bigl( 1 - (-1) \bigr) = \frac13. \end{equation*}\] Thus, for the uniform kernel we have \[\begin{equation*} R(K)^2 \mu_2(K) = \Bigl( \frac12 \Bigr)^2 \frac13 = \frac{1}{12} \approx 0.083333. \end{equation*}\]

Calculations similar to the ones in the example give the following values:

kernel \(\mu_2(K)\) \(R(K)\) \(R(K)^2 \mu_2(K)\)
Uniform 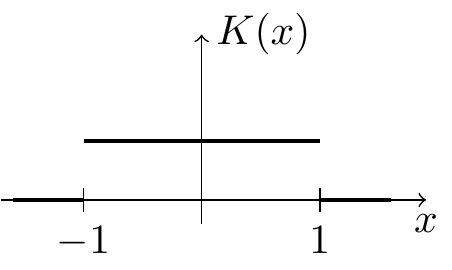uniform kernel \(\displaystyle\frac13\) \(\displaystyle\frac12\) \(0.08333\)
Triangular 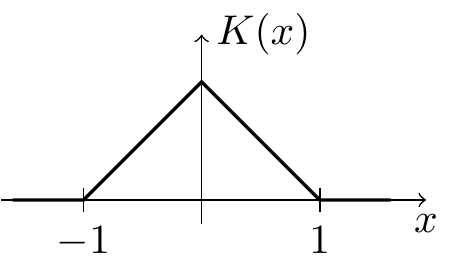triangluar kernel \(\displaystyle\frac16\) \(\displaystyle\frac23\) \(0.07407\)
Epanechnikov 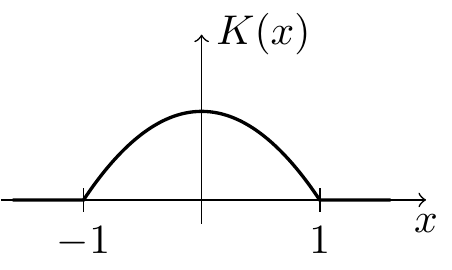Epanechnikov kernel \(\displaystyle\frac15\) \(\displaystyle\frac35\) \(0.07200\)
Gaussian 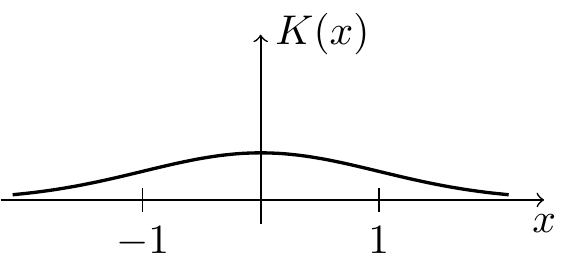Gaussian kernel \(1\) \(\displaystyle\frac{1}{2\sqrt{\pi}}\) \(0.07958\)

The best value in the table is obtained for the Epanechnikov kernel, with \(R(K)^2 \mu_2(K) = 9/125 = 0.072\). One can show that this value is indeed optimal amongst all kernels. Since the difference in error for the kernels listed above is only a few percent, any of these kernels would be a reasonable choice.

3.3 Bandwidth Selection

Our formulas for the optimal bandwidth contain the terms \(f(x)^2 |f''(x)|\) for fixed \(x\) and \(R(f'')\) for the integrated error. Since \(f\) is unknown, neither of these quantities are available and instead different rules of thumb are used in the literature. Here we present one possible choice of bandwidth estimator.

Suppose that \(f\) is a normal density, with mean \(\mu\) and variance \(\sigma^2\). Then we have \[\begin{equation*} f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\bigl( - (x-\mu)^2 / 2\sigma^2 \bigr). \end{equation*}\] Taking derivatives we get \[\begin{equation*} f'(x) = - \frac{1}{\sqrt{2\pi\sigma^2}} \frac{x-\mu}{\sigma^2} \exp\bigl( - (x-\mu)^2 / 2\sigma^2 \bigr) \end{equation*}\] and \[\begin{equation*} f''(x) = \frac{1}{\sqrt{2\pi\sigma^2}} \Bigl( \frac{(x-\mu)^2}{\sigma^4} - \frac{1}{\sigma^2} \Bigr) \exp\bigl( - (x-\mu)^2 / 2\sigma^2 \bigr) \end{equation*}\] Patiently integrating the square of this function gives \[\begin{equation*} R(f'') = \int_{-\infty}^\infty f''(x)^2 \,dx = \cdots = \frac{3}{8\sigma^5\sqrt{\pi}}. \end{equation*}\] This can be used as a simple “plug-in rule” with \(\sigma\) estimated by the sample standard deviation.

We now demonstrate how this rule of thumb could be used in R to obtain a kernel density estimate for the snowfall data. We will use the Epanechnikov kernel. For compatibility with the kernels built into R, we rescale this kernel, so that \(\mu_2(K) = 1\), i.e. we consider \(K_{\sqrt{5}}\) in place of \(K\). An easy calculation shows that the roughness is then \(R(K) = 3 / (5*\sqrt(5))\).

# downloaded from https://teaching.seehuhn.de/data/buffalo/
x <- read.csv("data/buffalo.csv")
snowfall <- x$snowfall
n <- length(snowfall)

# Roughness of the Epanechnikov kernel, after rescaling with h = sqrt(5)
# so that the second moment becomes mu_2 = 1:
R.K <- 3 / (5 * sqrt(5))

# Rule of thumb:
R.fpp <- 3 / (8 * sd(snowfall)^5 * sqrt(pi))

# formula for the optimal h
my.bw <- (R.K / (n * 1^2 * R.fpp))^0.2
my.bw
## [1] 11.58548

R has a variety of different builtin methods to estimate bandwidths. See stats/bandwidth for a description. For comparison to our result, we list here the bandwidths suggested by some of R’s algorithms:

data.frame(
  name = c("nrd0", "nrd", "SJ"),
  bw = c(bw.nrd0(snowfall), bw.nrd(snowfall), bw.SJ(snowfall)))
##   name        bw
## 1 nrd0  9.724206
## 2  nrd 11.452953
## 3   SJ 11.903840

All of these value seem close the value we obtained manually. Using our bandwidth estimate, we get the following estimated density.

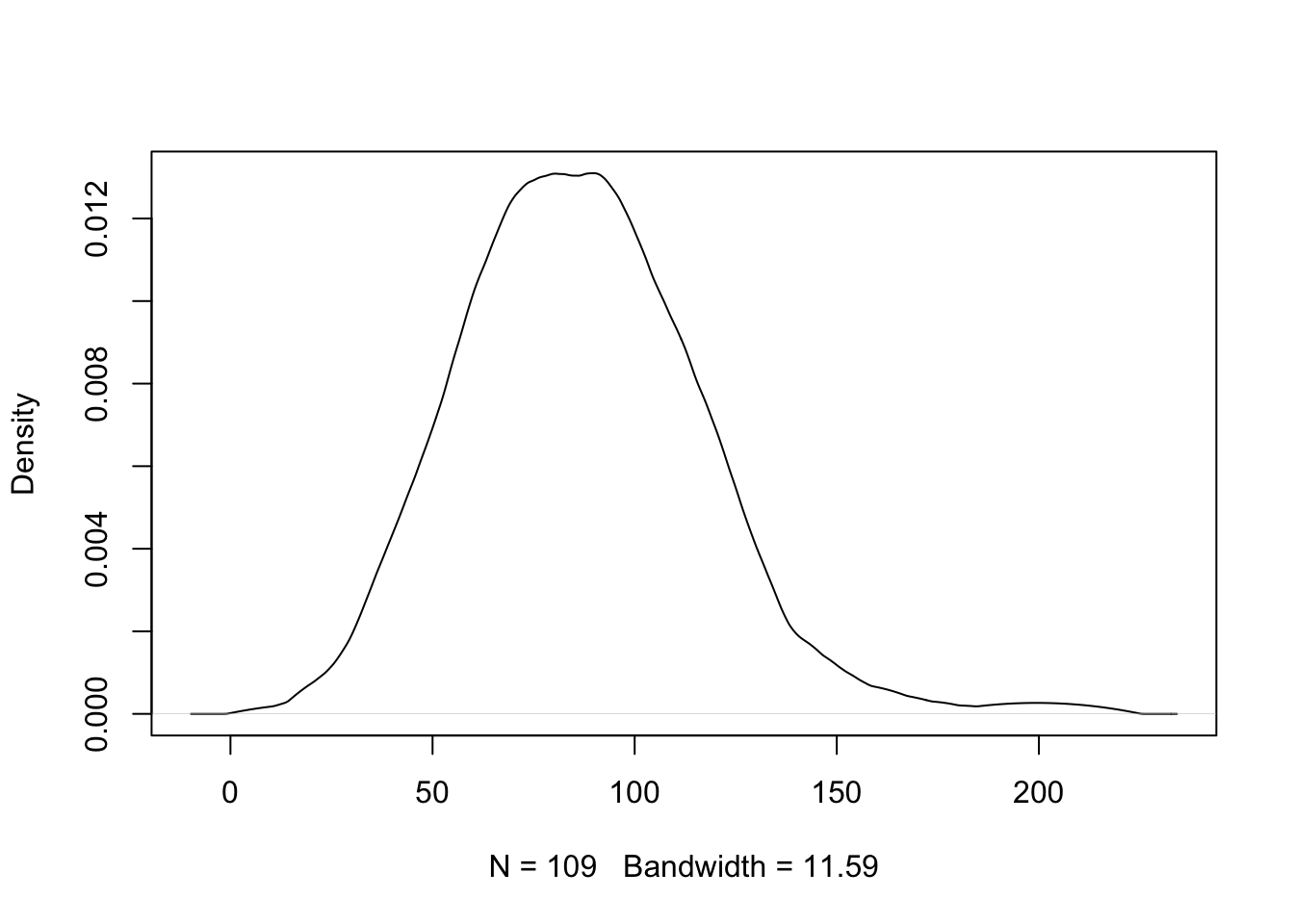
plot(density(snowfall, bw = my.bw, kernel = "epanechnikov"),
     main = NA)

In practice one would just use one of the built-in methods, for example using bw="SJ" instead of estimating the bandwidth manually.

3.4 Higher Dimensions

So far we have only considered the one-dimensional case, where the samples \(x_i\) are real numbers. In this subsection we will sketch how these methods will need to be adjusted for the multivariate case of \(x_i = (x_{i,1}, \ldots, x_{i,p}) \in \mathbb{R}^p\).

In this setup, a kernel is a function \(K\colon \mathbb{R}^p\to \mathbb{R}\) such that

  • \(\int \cdots \int K(x) \,dx_p \cdots dx_1 = 1\),
  • \(K(x) = K(-x)\) and
  • \(K(x) \geq 0\) for all \(x\in \mathbb{R}\),

where the integral in the first condition is now over all \(p\) coordinates.

Example 3.2 If \(K_1, \ldots, K_p\) are one-dimensional kernels, then the product \[\begin{equation*} K(x_1, \ldots, x_p) := K_1(x_1) \cdots K_p(x_p) \end{equation*}\] is a kernel in \(p\) dimensions. If we use the product of \(p\) Gaussian kernels, we get \[\begin{align*} K(x) &= \prod_{i=1}^p \frac{1}{\sqrt{2\pi}} \exp\bigl(-x_i^2/2\bigr) \\ &= \frac{1}{(2\pi)^{p/2}} \exp\Bigl(-\frac12 (x_1^2 + \cdots + x_p^2) \Bigr). \end{align*}\]

There are different possibilities for rescaling these kernels:

  • If all coordinates live on “comparable scales” (e.g., if they are measured in the same units), the formula \[ K_h(x) = \frac{1}{h^p} K(x/h) \] for all \(x\in\mathbb{R}^p\) can be used, where \(h>0\) is a bandwidth parameter as before. The scaling by \(1/h^p\) is required to ensure that the integral of \(K_h\) equals \(1\), so that \(K_h\) is a kernel again.

  • If different scaling is desirable for different components, the formula \[\begin{equation*} K_h(x) = \frac{1}{h_1 \cdots h_p} K(x_1/h_1, \ldots, x_p/h_p) \end{equation*}\] for all \(x\in\mathbb{R}^p\) can be used, where \(h = (h_1, \ldots, h_p)\) is a vector of bandwidth parameters.

  • A more general version would be to use a symmetric, positive definite bandwidth matrix \(H \in \mathbb{R}^{p\times p}\). In this case the required scaling is \[\begin{equation*} K_H(x) = \frac{1}{\mathrm{det}(H)} K\bigl( H^{-1} x \bigr) \end{equation*}\] for all \(x\in\mathbb{R}^p\).

For all of these choices, the kernel density estimator is given by \[\begin{equation*} \hat f_h(x) = \frac{1}{n} \sum_{i=1}^n K_h(x - x_i) \end{equation*}\] (using \(K_H\) for the third option) for all \(x\in\mathbb{R}^p\). Bandwidth selection in the multivariate case is a difficult problem and we will not discuss this here.